Implementing the Model

important

Before following the tutorial, you should have:

• PyTorch installed in your machine. Read instructions here.
• CSV file with dataset from Preparing Dataset for PyTorch.

Matrix Factorization Model in PyTorch

Taking the idea of Matrix Factorization, let's implement this in PyTorch.

First, let's import some necessary modules.

import torch

import torch.nn as nn

import torch.nn.functional as F

from sklearn.model_selection import train_test_split

Next, let's build our Matrix Factorization Model class.

class MF(nn.Module):

def __init__(self, num_users, num_items, emb_size=100):

super(MF, self).__init__()

self.user_emb = nn.Embedding(num_users, emb_size)

self.item_emb = nn.Embedding(num_items, emb_size)

# initializing our matrices with a positive number generally will yield better results

self.user_emb.weight.data.uniform_(0, 0.5)

self.item_emb.weight.data.uniform_(0, 0.5)

def forward(self, u, v):

u = self.user_emb(u)

v = self.item_emb(v)

return (u*v).sum(1) # taking the dot product

To instantiate our model, we can simply call on it like so:

note

The variables num_users and num_items represent the number of unique users and unique items in the dataset respectively.

model = MF(num_users, num_items, emb_size=100)

Currently, this is what the dataset looks like:

The items here are games that we want to recommend to users.

Once the model is instantiated, we can proceed to split our dataset to train and test our model. The general split is 20% test and 80% training.

train_df, valid_df = train_test_split(dataset, test_size=0.2)

# resetting indices to avoid indexing errors

train_df = train_df.reset_index(drop=True)

test_df = valid_df.reset_index(drop=True)

Now, we want to create our training function to train the model.

def train_epocs(model, epochs=10, lr=0.01, wd=0.0):

optimizer = torch.optim.Adam(model.parameters(), lr=lr, weight_decay=wd)

model.train()

for i in range(epochs):

usernames = torch.LongTensor(train_df.UserId.values)

game_titles = torch.LongTensor(train_df.TitleId.values)

ratings = torch.FloatTensor(train_df.Userscore.values)

y_hat = model(usernames, game_titles)

loss = F.mse_loss(y_hat, ratings)

optimizer.zero_grad() # reset gradient

loss.backward()

optimizer.step()

print(loss.item())

test(model)

In each iteration, the training function is updating our model to approach a smaller MSE (mean squared error). This is the idea of gradient descent.

And finally, we want to create our test function, which will be called right after training is done.

def test(model):

model.eval()

usernames = torch.LongTensor(test_df.UserId.values)

game_titles = torch.LongTensor(test_df.TitleId.values)

ratings = torch.FloatTensor(test_df.Userscore.values)

y_hat = model(usernames, game_titles)

loss = F.mse_loss(y_hat, ratings)

print("test loss %.3f " % loss.item())

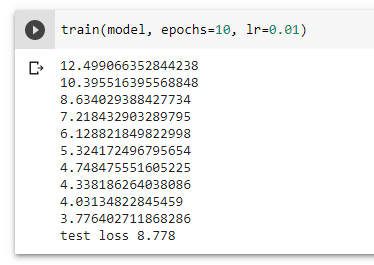
We can see that although our model's lowest MSE in our training dataset was about 3.776, the actual MSE based on our test dataset is about 8.778. Generally, this is a normal result, but a big difference between the training and test MSE likely suggests that our model is overfitted.

Model Prediction

And now, we are ready to use our model for prediction! For example, to predict the ratings of games for user of user id 10, we can run the following lines:

user = torch.tensor([10])

games = torch.tensor(game_ratings['TitleId'].unique().tolist())

predictions = model(user, games).tolist()

print(predictions)

Notice that some of the predictions went over 10. To fix this, we can simply normalize our results like so:

normalized_predictions = [i/max(predictions)*10 for i in predictions]

print(normalized_predictions)

Finally, we can recommend some games by sorting our predictions list:

sortedIndices = predictions.argsort()

recommendations = dataset['Title'].unique()[sortedIndices][:30] # taking top 30 games

print(recommendations)